Answer:
C. 29.8 inches
Explanation:
Length of complete hula hoop(L)= circumference of hoop
=>
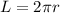
where radius, r= 19 inches
Therefore length of arc(l) subtending 1/4 of the hoop is
=>
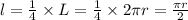
=>
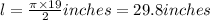
Thus the length of the arc subtending 1/4 of the hoop is 29.8 inches