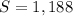Answer:
The sum of the first twenty-seven terms is 1,188
Explanation:
we know that
The formula of the sum in arithmetic sequence is equal to
![S=(n)/(2)[2a1+(n-1)d]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/j8ryiskp88qqeevz0hq45lzgu3onrq8mx3.png)
where
n is the number of terms
a1 is the first term
d is the common difference (constant)
step 1
Find the common difference d
we have
n=7
a1=-8
S=28
substitute and solve for d
![28=(7)/(2)[2(-8)+(7-1)d]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/atzopl7b4b05z386pzv10giqvt7jyavfub.png)
![28=(7)/(2)[-16+(6)d]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/o3a8frsclxyw9c2ztvnmckozrhzxk63dka.png)
![8=[-16+(6)d]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6nrdbdrr1fl03qp6o9xj8bmzxcvajxujyu.png)
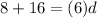
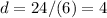
step 2
Find the sum of the first twenty-seven terms
we have
n=27
a1=-8
d=4
substitute
![S=(27)/(2)[2(-8)+(27-1)(4)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/w1qz1hbrj3qhny9hb69f0p4svc7bnzx4hr.png)
![S=(27)/(2)[(-16)+(104)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kp9e65hcatarej8g5m328ufbx57nyld7kx.png)
![S=(27)/(2)88]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/p3qvgfc9wx06bcy1a3xhmv3mh9zwbzjmkx.png)