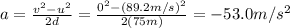Question

In January 2004, NASA landed exploration vehicles on Mars. Part of the descent consisted of the following stages:

Stage A: Friction with the atmosphere reduced the speed from 19300 km/h to 1600 km/h in 4.0 min.
Stage B: A parachute then opened to slow it down to 321 km/h in 94 s.
Stage C: Retro rockets then fired to reduce its speed to zero over a distance of 75 m.
Assume that each stage followed immediately after the preceding one and that the acceleration during each stage was constant.

1- Find the rocket's acceleration (in m/s2) during stage A

2- Find the rocket's acceleration (in m/s2) during stage B

3-Find the rocket's acceleration (in m/s2) during stage C

Answer 1

Acceleration is given by:

`a=(v-u)/(t)`

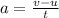
where

v is the final velocity

u is the initial velocity

t is the time interval

Let's apply the formula to the different parts of the problem:

A)
`-20.5 m/s^2`

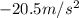
Let's convert the quantities into SI units first:

`u = 19300 km/h \cdot (1000 m/km)/(3600 s/h) = 5361.1 m/s`

`v=1600 km/h  \cdot (1000 m/km)/(3600 s/h)  =444.4 m/s`

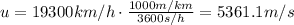
t = 4.0 min = 240 s

So the acceleration is

`a=(444.4 m/s-5361.1 m/s)/(240 s)=-20.5 m/s^2`

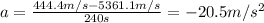
B)
`-3.8 m/s^2`

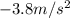
As before, let's convert the quantities into SI units first:

`u = 444.4 m/s`

`v=321 km/h  \cdot (1000 m/km)/(3600 s/h)  =89.2 m/s`

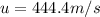
t = 94 s

So the acceleration is

`a=(89.2 m/s - 444.4 m/s)/(94 s)=-3.8 m/s^2`

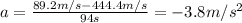
C)
`-53.0 m/s^2`

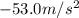
For this part we have to use a different formula:

`v^2 - u^2 = 2ad`

where we have

v = 0 is the final velocity

u = 89.2 m/s is the initial velocity

a is the acceleration

d = 75 m is the distance covered

Solving for a, we find

`a=(v^2-u^2)/(2d)=(0^2-(89.2 m/s)^2)/(2(75 m))=-53.0 m/s^2`