Question

What are the x-intercepts of f(x) = x2 + 6x + 5 ?

Answer 1

`x = -5\\x = -1`

Explanation:

To find the intercept with the x axis, you must do
`f(x) = 0`

So:

`f(x) = x^2 + 6x + 5 = 0`

Now you must factor the expression.

To factor the expression you must find two numbers such that when you add them, you obtain 6 and multiplying it will result in 5.

You can verify that these numbers are 5 and 1.

So

`f(x) = (x + 5)(x + 1) = 0`

Therefore the solutions are

`x = -5\\x = -1`

Answer 2

Hello!

The answer is:

The x-intercept or roots of the parabola are:

`x_(1)=-5\\x_(2)=-1`

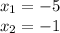
Why?

To solve the problem, we need to find the roots or zeroes of the parabola.

We can find the zeroes of the quadratic equation (parabola) by factoring its equation.

So,we are given the function:

`f(x)=x^(2) +6x+5`

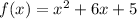
To factorize the equation, we need to find two numbers which product gives as result the number 5, and its addition gives as result the number "6", these numbers are 5 and 1.

So, rewriting the equation, we have:

`f(x)=x^(2) +6x+5=(x+5)(x+1)=0`

Therefore, we have that the x-intercept or roots of the parabola are:

`x_(1)=-5\\x_(2)=-1`

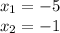
Have a nice day!

Note: I have attached a picture for better understanding.