Answer:
Option 'B'
Explanation:
The law of cosines states that given a triangle with sides a, b, c, then:
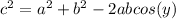 where 'y' is the opposite angle to the side 'c'.
where 'y' is the opposite angle to the side 'c'.
In this case, given that the equation is:
 we can clearly see that c=15, and the opposite angle to 'c' is 62 degrees.
we can clearly see that c=15, and the opposite angle to 'c' is 62 degrees.
The correct option is Option 'B'