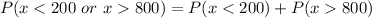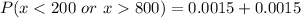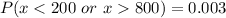Question

A college-entrance exam is designed so that scores are normally distributed with a mean of 500 and a standard deviation of 100. Using the eight‐part symmetry of the area under a normal curve, what is the probability that a randomly chosen exam score is less than 200 or greater than 800?

The probability is__?

Answer 1

The probability is 0.003

Explanation:

We know that the average
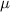`\mu` is:

`\mu=500`

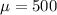
The standard deviation
`\sigma` is:

`\sigma=100`

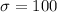
The Z-score is:

`Z=(x-\mu)/(\sigma)`

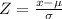
We seek to find

`P(x<200\ or\ x>800)`

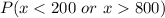
For P(x>800) The Z-score is:

`Z=(x-\mu)/(\sigma)`

`Z=(800-500)/(100)`

`Z=3`

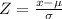
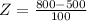
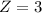
The score of Z = 3 means that 800 is 3 standard deviations from the mean. Then by the rule of the 8 parts of the normal curve, the area that satisfies the conficion of 3 deviations from the mean has percentage of 0.15%

So

`P(x>800)=0.15\%`

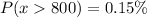
For P(x<200) The Z-score is:

`Z=(x-\mu)/(\sigma)`

`Z=(200-500)/(100)`

`Z=-3`

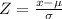
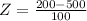
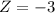
The score of Z = -3 means that 200 is 3 standard deviations from the mean. Then by the rule of the 8 parts of the normal curve, the area that satisfies the conficion of 3 deviations from the mean has percentage of 0.15%

So

`P(x<200)=0.0015`

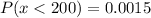
Therefore

`P(x<200\ or\ x>800)=P(x<200) +P(x>800)`

`P(x<200\ or\ x>800)=0.0015 + 0.0015`

`P(x<200\ or\ x>800)=0.003`