Question

The measure of angle zero is 600°. The point XY corresponding to zero on the unit circle is

Answer 1

`x= -(1)/(2)\\\\ y= -(√(3))/(2)`

Explanation:

We are given that the measure of angle θ is 600° and we are to fin the point (x, y) corresponding to angle θ on the unit circle,

We know that the x,y coordinates in the unit circle are the cosine and sine ratios, respectively.

θ = 600

1 unit circle= 360°

It means that 600° corresponds to 600° - 360° = 240°.

So, θ = 360° + 240°

180° < 240° < 270° (this tells that the point is in the third quadrant and its coordinates are negative)

240° - 180° = 60° (using the supplementary angles to find the sin and cos)
`\sin 60^\circ = (√(3))/(2)\\\\\cos 60^\circ= (1)/(2)`

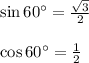
Therefore, the x-coordinate is the cos of the given angle while y-coordinate is the sine of the given angle and the coordinates are:

`x= -(1)/(2)\\\\ y= -(√(3))/(2)`