y = 6x - 2. The equation that describes how x and y are related is given by y = 6x - 2.
If we look the table of the image, we can see that the graph that describes the relation between x and y is a straight line.
The set of infinite points aligned in the same direction is known as straight line and its main equation has the form y = mx + b, where m is the slope, and b the y-intercept.
In order to solve this problem, we need to find the slope which is
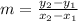
Solving m for two points of the straight line, Let's take (0, -2) and (1, 4):
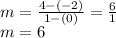
We can see if we take two points in order from the table always obtain the value m = 6, which means for each unit of x, y increase 6 units.
To find the y- intercept (0, y), from the table of the image we can see when x = 0, y = -2.
Writing the equation y = mx + b, with m = 6 and b = -2:
y = 6x -2