Question

A quadrilateral is graphed in the coordinate plane below. Which classification best describes the quadrilateral (parallelogram, rhombus, etc.)?

Answer 1

Trapezoid

Explanation:

Given quadrilateral has vertices at points A(-2,-1), B(3,13), C(15,5) and D(13,-11).

Find slopes of lines AD and BC:

`\text{Slope}_(AD)=(y_D-y_A)/(x_D-x_A)=(-11-(-1))/(13-(-2))=(-11+1)/(13+2)=(-10)/(15)=-(2)/(3)\\ \\\text{Slope}_(BC)=(y_C-y_B)/(x_C-x_B)=(5-13)/(15-3)=(-8)/(12)=-(2)/(3)`

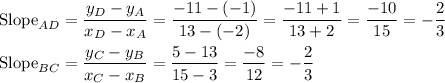
Since the slopes are the same, lines AD and BC are parallel.

Find slopes of lines ABD and CD:

`\text{Slope}_(AB)=(y_B-y_A)/(x_B-x_A)=(13-(-1))/(3-(-2))=(14)/(5)\\ \\\text{Slope}_(CD)=(y_D-y_C)/(x_D-x_C)=(-11-5)/(13-15)=(-16)/(-2)=8`

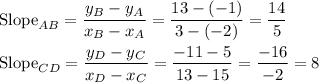
Since the slopes are different, lines AB and CD are not parallel.

This means quadrilateral ABCD is trapezoid (two opposite sides - parallel and two another opposite sides - not parallel)