Question

Homogenuos function who can solve it

Answer 1

a) f(x) is a homogenous function of degree '1'

b) f(x) is a homogenous function of degree '2'

Explanation:

Step(i):-

Homogenous function

If f(x) is a homogenous function of degree 'n' then

`f(k x ,k y) = k^(n) f(x, y)`

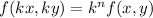
a)

Given
`f(x, y) = \sqrt{x^(2) +3xy+2y^(2) }`

`f(kx, ky) = \sqrt{(kx)^(2) +3kx(ky)+2(ky)^(2) }`

`f(kx, ky) = \sqrt{(k)^(2) (x)^(2) +3k^(2) (xy)+2(k)^(2) y^(2) }`

`f(kx, ky) =( k^(2))^{(1)/(2) } ( \sqrt{(x)^(2) +3 (xy)+2 y^(2) })`

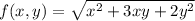
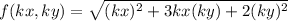
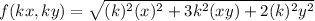
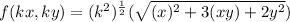
f( k x , k y ) = k f( x, y)

∴ f(x) is a homogenous function of degree '1'

Step(ii):-

b)

`f(x, y) = \sqrt{x^(4) +3x^(2) y+5y^(2) x^(2) -2y^(4) }`

`f(kx, ky) = \sqrt{(k x)^(4) +3(k x)^(2) y+5(k y)^(2) (k x)^(2) -2(k y)^(4) }`

`f(kx, ky) = (k^(4))^{(1)/(2) } \sqrt{( x)^(4) +3( x)^(3) y+5( y)^(2) ( x)^(2) -2( y)^(4) }`

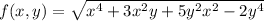
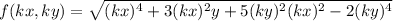
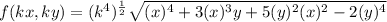
f(k x , k y ) = k² f( x , y )

∴ f(x) is a homogenous function of degree '2'