Question

Combine the following expressions:

Answer 1

`(4n - 1)√(3 n) + 3√(n)`

EXPLANATION

The given expression is

`\sqrt{48 {n}^(3) } + √(9n) - √(3n)`

We remove the perfect squares under the radical sign.

`\sqrt{16 {n}^(2) *3 n} + √(9n) - √(3n)`

We can now take square root of the perfect squares and simplify them further.

`\sqrt{16 {n}^(2)} * √(3 n) + √(9) * √(n) - √(3n)`

This simplifies to:

`4n√(3 n) + 3√(n) - √(3n)`

This further simplifies to:

`(4n - 1)√(3 n) + 3√(n)`

Answer 2

Option B is Correct

Explanation:

`√(48n^3)+√(9n) - √(3n)`

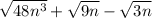
We need to solve the above expression.

48 can be written as: 2x2x2x2x3

9 can be written as : 3x3

Putting values

`√(2*2*2*2*3*n*n*n) +√(3*3*n)-√(3n)`

2*2 = 2^2 and n*n = n^2 and 3*3 = 3^2

we also know √ = 1/2

so, putting these values we get,

`√(2^2*2^2*3*n^2*n) +√(3^2*n)-√(3n)\\(2^2)^(1/2) * (2^2)^(1/2) * (3)^(1/2) * (n^2)^(1/2) * n ^(1/2) + ((3^2)^(1/2) *n^(1/2)) -(√(3n))\\2*2*n * (3^(1/2) *n ^(1/2)) +(3 +n^(1/2)) -(√(3n))\\4n (√(3n))+(3 √(n)) -(√(3n))\\Rearraninging\\4n(√(3n)) - (√(3n))+(3 √(n))\\Taking \,\,√(3n) \,\,common\,\, from\,\, 1st\,\, and\,\, 2nd\,\, term\\√(3n)(4n-1)+(3 √(n))\\or \,\,it\,\,can\,\,be\,\,written\,\,as\,\,\\(4n-1)√(3n)+(3 √(n))`

So, Option B is Correct.