Answer:
Option B is Correct
Explanation:
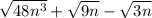
We need to solve the above expression.
48 can be written as: 2x2x2x2x3
9 can be written as : 3x3
Putting values
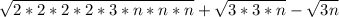
2*2 = 2^2 and n*n = n^2 and 3*3 = 3^2
we also know √ = 1/2
so, putting these values we get,
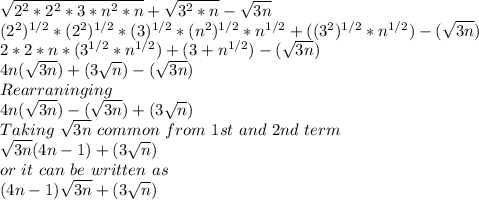
So, Option B is Correct.