Question

the function f(x)= 3x squared+12x+11 can be written in vertex form as A. f(x)=(3x+6) squared-25 B. f(x)=3(x+6) squared-25 C. f(x)= 3(x+2) squared-1 D. f(x)= 3(x+2) squared+7) explain and show your work ​and what is vertex form

Answer 1

`\boxed{\text{C. }{f(x) =3(x + 2)^(2) - 1}}`

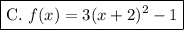
Explanation:

The vertex form of a quadratic function

ƒ(x) = a(x - h)² + k, where (h, k) is the vertex of the parabola.

You convert ƒ(x) = 3x² + 12x + 11 to the vertex form by completing the square.

Step 1. Move the constant term to the other side of the equation

y - 11 =3x² + 12x

Step 2. Factor out the leading coefficient

y - 11 =3(x² + 4x)

Step 3. Complete the square on the right-hand side

Take half the coefficient of x, square it, and add it to each side of the equation.

4/2 = 2; 2² = 4

y – 11 + 12 =3(x² + 4x + 4)

Note that when you completed the square by adding 4 inside the parentheses, you were adding 3×4 to the right-hand side, so you had to add 12 to the left-hand side.

Step 4. Simplify and write the right-hand side as a perfect square

y + 1 = 3(x + 2)²

Step 5. Isolate the y term

Subtract 1 from each side

y = 3(x + 2)² -1

`\text{The vertex form of the equation is }\boxed{\mathbf{f(x) =3(x + 2)^(2) - 1}}`

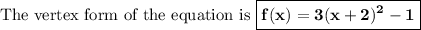
If you compare this equation with the general vertex form and with the graph, you will find that h = -2 and k = -1, so the vertex is at (-2, -1).