Question

PLEASE HELP Match each function formula with the corresponding transformation of the parent function y = - (x + 2)2. 1. y = - (x + 4)2 Reflected across the x-axis and the y-axis 2. y = - (x + 2)2 - 2 Translated right by 2 units 3. y = (x - 2)2 Translated left by 2 units 4. y = 2 - (x + 2)2 Translated down by 2 units 5. y = -x2 Translated up by 2 units 6. y = (x + 2)2 Reflected across the x-axis

Answer 1

So we are given the following function:
`y=-(x + 2)^(2)`.

Before we can solve this problem, we need to know the following:

• Given g (x) = f (x) + k; The graph of g(x) equals f(x) shifted k units vertically. If k > 0, the base graph shifts k units upward, and if k < 0, the base graph shifts k units downward.

• Given g(x) = f (x - k); The graph of g(x) equals f(x) shifted k units horizontally. If k > 0, the base graph shifts k units to the right, and if k < 0, the base graph shifts k units to the left.

• The reflection of the point (x,y) across the x-axis is the point (x,-y).

• The reflection of the point (x,y) across the y-axis is the point (-x,y).

Know we can solve the problem!

1.
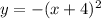`y=-(x + 4)^(2)`. Translated left by 2 units.

2.
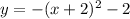`y=-(x + 2)^(2) - 2` Translated down by 2 units

3.
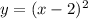`y=(x - 2)^(2)` Reflected across the x-axis and the y-axis

4.
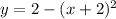`y= 2-(x + 2)^(2)` Translated up by 2 units

5.
`y=-(x)^(2)` Translated right by 2 units

6.
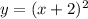`y=(x + 2)^(2)` y = (x + 2)2 Reflected across the x-axis