Question

Vance is designing a garden in the shape of an isosceles triangle. The base of the garden is 30 feet long. The function y = 15 tan θ models the height of the triangular garden. What is the height of the triangle when θ = 30 ° ? What is the height of the triangle when θ = 40 ° ? Vance is considering using either θ = 30 ° or θ = 40 ° for his garden. Compare the areas of the two possible gardens. Explain how you found the areas.

Answer 1

Part 1) The height of the triangle when θ = 30° is equal to
`8.66\ ft`

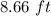
Part 2) The height of the triangle when θ = 40° is equal to
`12.59\ ft`

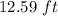
Part 3) The area of triangle with θ = 30° is less than the area of triangle with θ = 40°

Explanation:

Part 1) What is the height of the triangle when θ = 30 ° ?

we have

`y=15tan(\theta)`

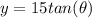
substitute the value of theta in the equation and find the height

`y=15tan(30\°)=8.66\ ft`

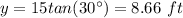
Part 2) What is the height of the triangle when θ = 40 ° ?

we have

`y=15tan(\theta)`

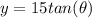
substitute the value of theta in the equation and find the height

`y=15tan(40\°)=12.59\ ft`

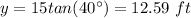
Part 2) Vance is considering using either θ = 30 ° or θ = 40 ° for his garden

Compare the areas of the two possible gardens

step 1

Find the area when θ = 30 °

The height is
`8.66\ ft`

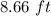
Remember that the area of a triangle is equal to the base multiplied by the height and divided by two

so

`A=(1/2)(30)(8.66)=129.9\ ft^(2)`

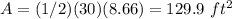
step 2

Find the area when θ = 40°

The height is
`12.59\ ft`

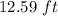
Remember that the area of a triangle is equal to the base multiplied by the height and divided by two

so

`A=(1/2)(30)(12.59)=188.85\ ft^(2)`

Compare the areas of the two possible gardens

The area of triangle with θ = 30° is less than the area of triangle with θ = 40°