Question

Two stores have movies to rent

The first store charges a $12.50-per-month membership fee plus
$1.50 per movie rented
The second store has no membership fee but charges $3.50 per movie
rented.
What is the minimum number of movies a person would need to rent in a month
for the first store to be a better deal?​

Answer 1

Answer:7

Explanation:

In the first store, you pay 12.5+1.5x per x movies

In the second store, you pay 3.5x per x movies

The first store offers a better deal when:

12.5 + 1.5x > 3.5x

12.5 > 2x

6.25 > x

Which means if you rent minimum 7 movies in month, you should go to the first store

Answer 2

7

Explanation:

We know that the first store charges $12.50 per month, which is a initial condition, and charges additionally $1.50 per movie, which is variable, this represents the ratio of change, so this can be expressed as

`\$12.50 + \$1.50x`

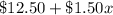
Where
`x` represents movies.

Now, the second store doesn't charge and membership fee, just it charges a cost per movie which is $3.50.

Then, to solve the minimum number of movies needed to Plan A be the best choice, we just have to solve the following inequality

`\$12.50 + \$1.50x> \$3.50`

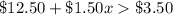
Which expresses the case where Plan A is a better choice, solving for
`x`, we have

`\$12.50 + \$1.50x> \$3.50x\\\$1.50x - \$3.50x >-\$12.50\\(-1)(-2x)>(-12.50)(-1)\\2x<12.50\\x<(12.50)/(2)\\ x<6.25`

Which means that the minimum number of movies is 7, which is the next whole number after 6.