Question

The function f(x) = 9.75x + 62 models the amount

of money that Hector earned working x hours in a
week. The function g(x) = 7.5x + 84 models the
amount of money that Cart earned working x
hours in the same week Which function, h(x).
models the difference in Hector's and Cari's
earnings?
a. h(x) = 17.25x - 22
b. h(x) = 17.25x + 146
c. h(x) = 2.25x - 22
d. h(x) = 2.25x + 146​

Answer 1

Answer: Option C

`h(x)=2.25x-22`

Explanation:

To find the function h(x) that models the difference between Hector's and Cari's gains, subtract the functions f(x) with g(x)

That is to say:

`h (x) = f (x) -g (x)`

We know that

`f (x) = 9.75x + 62\\\\g (x) = 7.5x + 84`

Then we can find the function h(x)

`h(x) = 9.75x + 62 - (7.5x + 84)\\\\h(x) = 9.75x + 62 -7.5x -84`

`h(x)=2.25x-22`

Answer 2

Hello!

The answer is:

The third option,

c)
`h(x)=2.25x-22`

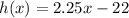
Why?

We are given the functions E(x) and K(x), since they both are function of the same variable, we need to calculate the difference between them.

From the statement we know the functions:

`f(x)=9.75x+62`

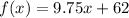
and

`g(x)=7.5x+84`

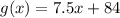
So, calculating the difference the functions we have:

`h(x)=f(x)-g(x)`

`h(x)=(9.75x+62)-(7.5x+84)`

`h(x)=(9.75x+62)-(7.5x+84)`

`h(x)=9.75x-7.5x+62-84`

`h(x)=2.25x-22`

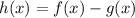
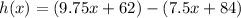
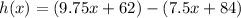
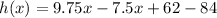
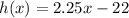
Hence, the answer is the third option,

c)
`h(x)=2.25x-22`

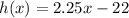
Have a nice day!