Question

Find the missing lengths of the sides

Answer 1

The correct answer is C

EXPLANATION

The side adjacent to the 60° angle is 8 units.

The hypotenuse is c.

Using the cosine ratio, we have

`\cos(60 \degree) = (adjacent)/(hypotenuse)`

`\cos(60 \degree) = (8)/(c)`

`(1)/(2)= (8)/(c)`

Cross multiply

`c = 8 * 2 = 16`

Also

`\cos(30 \degree) = (b)/(c)`

`\cos(30 \degree) = (b)/(16)`

`( √(3) )/(2) = (b)/(16)`

Multiply both sides by 16

`b = 16 * ( √(3) )/(2)`

`b = 8 √(3)`

The correct answer is C

Answer 2

Answer: option c

Explanation:

You can use these identities:

`sin\alpha=(opposite)/(hypotenuse)\\\\tan\alpha=(opposite)/(adjacent)`

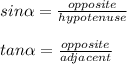
Then, using the angle that measures 30 degrees, you know that:

`\alpha=30\°\\opposite=8\\adjacent=b`

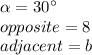
Substituting:

`tan(30\°)=(8)/(b)`

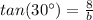
Now you must solve for b:

`b=(8)/(tan(30\°))\\\\b=8√(3)`

Using the angle that measures 30 degrees, you know that:

`\alpha=30\°\\opposite=8\\hypotenuse=c`

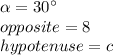
Substituting:

`sin(30\°)=(8)/(c)`

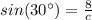
Now you must solve for c:

`c=(8)/(sin(30\°))\\\\c=16`