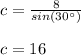Answer: option c
Explanation:
You can use these identities:
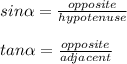
Then, using the angle that measures 30 degrees, you know that:
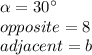
Substituting:
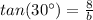
Now you must solve for b:
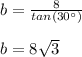
Using the angle that measures 30 degrees, you know that:
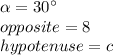
Substituting:
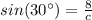
Now you must solve for c: