Question

A rock weighing 15.0 g is

placed in a graduated cylinder,
displacing the volume from
25.0 mL to 36.2 mL. What is
the density of the rock in
grams/cubic centimeter?

Answer 1

Answer:
`1.38(g)/(cm^3)`

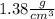
Explanation:

You need to remember the formula for calculate the density:

`density=(mass)/(volume)`

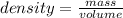
In this case:

`density_((rock))=(mass_((rock)))/(Volume_((rock)))`

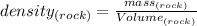
You know that:

`mass_((rock))=15.5g`

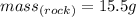
And when it is placed in a graduated cylinder, the volume is displaced from 25.0 mL to 36.2 mL.

Then, the volume of the rock is:

`Volume_((rock))=36.2mL-25.0mL=11.2mL`

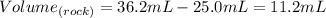
Since
`1mL=1cm^3`, you can rewrite the volume as:

`Volume_((rock))=11.2cm^3`

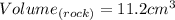
Substituting values into the formula, you get that the density of the rock is:

`density_((rock))=(15.5g)/(11.2cm^3)=1.38(g)/(cm^3)`