Question

Find the missing lengths of the sides

Answer 1

The correct answer is C

EXPLANATION

The given triangle is a right triangle. Since two angles are equal, it is a right isosceles triangle.

This implies that, x=8 units.

Using Pythagoras Theorem,

`{y}^(2) = {8}^(2) + {8}^(2)`

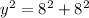
This implies that:

`{y}^(2) = 64 + 64`

`{y}^(2) =128`

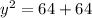
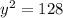
Take positive square root,

`{y} = √(128)`

`{y} = 8 √(2)`

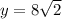
The correct answer is C

Answer 2

Correct choice is C.
`x=8`,
`y=8√(2)`.

Explanation:

Apply formula
`\sin\left(\theta\right)=(opposite)/(hypotenuse)`

`\sin\left(45^o\right)=(8)/(y)`

`(1)/(√(2))=(8)/(y)`

`y=8√(2)`

Apply formula
`\tan\left(\theta\right)=(opposite)/(adjacent)`

`\tan\left(45^o\right)=(8)/(x)`

`1=(8)/(x)`

`x=8`

Hence correct choice is C.
`x=8`,
`y=8√(2)`.