Question

Determine if the graph is symmetric about the x-axis, the y-axis, or the origin.

r = 4 cos 3θ

Answer 1

It is symmetric about the x-axis because cos(3θ) = cos(-3θ).

It is not symmetric about the y-axis because cos(3θ) is not equal to cos(3(pi-θ)).

It is not symmetric about the origin because cos(3θ) is not equal to -cos(3θ).

Answer 2

The graph is symmetric about x- axis.

Explanation:

We are given that an equation

`r=4 cos 3\theta`

We have to find the graph is symmetric about x- axis , y-axis or origin.

We taking r along y-axis and [tex\theta [/tex] along x- axis

When the graph is symmetric about x= axis then (x,y)=(-x,y)

`\theta` is replaced by
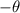`-\theta` and r remain same then we get

`r=4cos (-3\theta)`

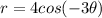
We know that cos (-x)=cos x

Therefore,
`r=4cos 3\theta`

Hence, the graph is symmetric about x- axis.

When the graph is symmetric about y- axis then (x,y)=(x,-y)

Now, r is replaced by -r then we get

`-r=4cos 3\theta`

`r=-4 cos {3\theta}`

`r=4 cos {\pi-3\theta}`

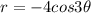
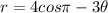
Therefore, the graph is not symmetric about y-axis.

When the graph is symmetric about y- axis then (x,y)=(x,-y)

Now, r is replaced by -r then we get

`-r=4cos 3\theta`

`r=-4 cos3\theta`

`r=4 cos (\pi-3\theta)`

`(\theta,r)\\eq (\theta,-r)`

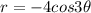
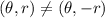
Therefore, the graph is not symmetric about y-axis.

When the graph is symmetric about origin then (-x,-y)=(x,y)

Replaced r by -r and
`\theta` by-
`\theta`

Then we get
`-r=4cos3(-\theta)`

`-r= 4 cos 3\theta`

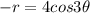
Because cos(-x)=cos x

`r=-4 cos 3\theta`

`(-\theta,-r)\\eq(\theta,r)`

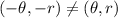
Hence, the graph is not symmetric about origin.