Answer:
The graph is symmetric about x- axis.
Explanation:
We are given that an equation
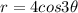
We have to find the graph is symmetric about x- axis , y-axis or origin.
We taking r along y-axis and [tex\theta [/tex] along x- axis
When the graph is symmetric about x= axis then (x,y)=(-x,y)
 is replaced by
is replaced by
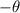 and r remain same then we get
and r remain same then we get
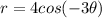
We know that cos (-x)=cos x
Therefore,
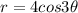
Hence, the graph is symmetric about x- axis.
When the graph is symmetric about y- axis then (x,y)=(x,-y)
Now, r is replaced by -r then we get
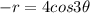
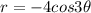
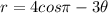
Therefore, the graph is not symmetric about y-axis.
When the graph is symmetric about y- axis then (x,y)=(x,-y)
Now, r is replaced by -r then we get
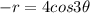
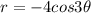
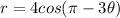
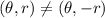
Therefore, the graph is not symmetric about y-axis.
When the graph is symmetric about origin then (-x,-y)=(x,y)
Replaced r by -r and
 by-
by-

Then we get
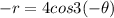
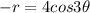
Because cos(-x)=cos x
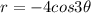
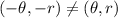
Hence, the graph is not symmetric about origin.