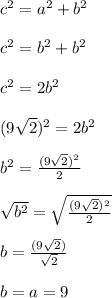Question

7.
Find the missing lengths of the sides.

Answer 1

x = 7, y = 9.9

Explanation:

Answer 2

`a=9\ in\\b= 9\ in`

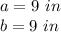
Explanation:

This straight triangle has two angles equal to 45 ° and two equal sides.

We know that the side opposite the 90 degree angle is:

`c =9√(2)\ in`

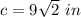
Since the triangle has two equal angles, then it is an iscoceles triangle.

This means that

`a = b`

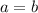
We use the Pythagorean theorem to find b

`c^2 = a^2 + b^2\\\\c^2 = b^2 + b^2\\\\c^2 = 2b^2\\\\(9√(2))^2 =2b^2\\\\b^2=((9√(2))^2)/(2)\\\\√(b^2)=\sqrt{((9√(2))^2)/(2)}\\\\b=((9√(2)))/(√(2))\\\\b=a=9`