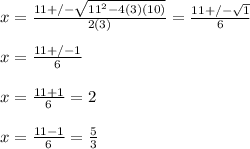Question

A quadratic equation is shown below:

3x2 − 11x + 10= 0

Part A: Find the vertex. Show your work.

Part B: Solve for x using an appropriate method. Show the steps of your work.

Answer 1

Part A:

( 1.8333, -0.08333)

Part B:

x = 2 or x = 5/3

Explanation:

The quadratic equation

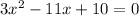`3x^(2)-11x+10=0` has been given.

Part A:

We are required to determine the vertex. The vertex is simply the turning point of the quadratic function. We shall differentiate the given quadratic function and set the result to 0 in order to obtain the co-ordinates of its vertex.

`(d)/(dx)(3x^(2)-11x+10)=6x-11`

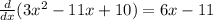
Setting the derivative to 0;

6x - 11 = 0

6x = 11

x = 11/6

The corresponding y value is determined by substituting x = 11/6 into the original equation;

y = 3(11/6)^2 - 11(11/6) + 10

y = -0.08333

The vertex is thus located at the point;

( 1.8333, -0.08333)

Find the attached

Part B:

We can use the quadratic formula to solve for x as follows;

The quadratic formula is given as,

`x=\frac{-b+/-\sqrt{b^(2)-4ac } }{2a}`

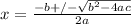
From the quadratic equation given;

a = 3, b = -11, c = 10

We substitute these values into the above formula and simplify to determine the value of x;

`x=\frac{11+/-\sqrt{11^(2)-4(3)(10) } }{2(3)}=(11+/-√(1) )/(6)\\\\x=(11+/-1)/(6)\\\\x=(11+1)/(6)=2\\\\x=(11-1)/(6)=(5)/(3)`