2 Answers

Cheemakurthi Mukesh · Answer 1 · 2020-09-02T14:39:24+0000

ANSWER

21

EXPLANATION

The given by binomial expression is:

$( {x}^(2) + y)^(7)$

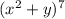
Comparing this to

(a+ b)^(n)

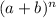
We have:

n = 7

$a = {x}^(2)$

b = y

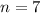
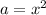
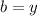
The coefficient of the (r+1)th term is given by:

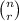
$\binom{n}{r}$

We want to find the coefficient of the third term:

r + 1 = 3

r = 2

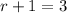
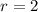
Therefore the coefficient is:

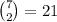
$\binom{7}{2} = 21$

The coefficient of the third term is 21.

Please log in or register to add a comment.