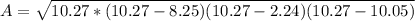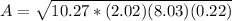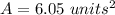Answer:
Part 2)
![P=2[√(20)+√(45)]\ units](https://img.qammunity.org/2020/formulas/mathematics/high-school/y05bjnmws6rwdfjjnczhyymiiwb21r51et.png) or
or
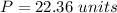
Part 4)
![P=[19+√(17)]\ units](https://img.qammunity.org/2020/formulas/mathematics/high-school/tlyghp7b3z3wxk22eve8z6bw3qigdhypcf.png) or
or
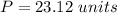
Part 6)
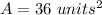
Part 8)

Part 10)
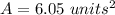
Step-by-step explanation:
we know that
The formula to calculate the distance between two points is equal to

Part 2) we have the rectangle ABCD
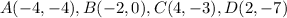
Remember that in a rectangle opposite sides are congruent
step 1
Find the distance AB
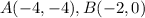
substitute in the formula
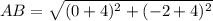
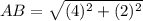

step 2
Find the distance BC
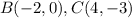
substitute in the formula
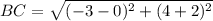
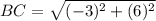
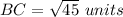
step 3
Find the perimeter
The perimeter is equal to
![P=2[AB+BC]](https://img.qammunity.org/2020/formulas/mathematics/high-school/pkwip896c5t82ubwr56fn1a1leluq1y2l1.png)
substitute
![P=2[√(20)+√(45)]\ units](https://img.qammunity.org/2020/formulas/mathematics/high-school/y05bjnmws6rwdfjjnczhyymiiwb21r51et.png)
or
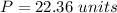
Part 4) we have the quadrilateral ABCD
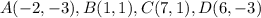
step 1
Find the distance AB

substitute in the formula
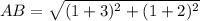
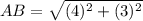
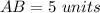
step 2
Find the distance BC

substitute in the formula
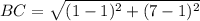
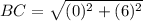
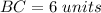
step 3
Find the distance CD
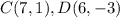
substitute in the formula
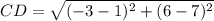
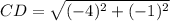

step 4
Find the distance AD
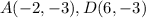
substitute in the formula
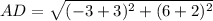
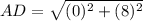
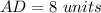
step 5
Find the perimeter
The perimeter is equal to
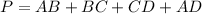
substitute
![P=[5+6+√(17)+8]\ units](https://img.qammunity.org/2020/formulas/mathematics/high-school/70cwp56qxmvgxujdcbssm0u09zycj1iiku.png)
![P=[19+√(17)]\ units](https://img.qammunity.org/2020/formulas/mathematics/high-school/tlyghp7b3z3wxk22eve8z6bw3qigdhypcf.png)
or
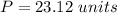
Part 6) Calculate the area of rectangle ABCD
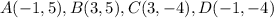
Remember that in a rectangle opposite sides are congruent
step 1
Find the distance AB
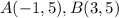
substitute in the formula

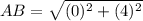
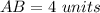
step 2
Find the distance BC
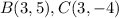
substitute in the formula

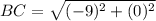

step 3
Find the area
The area is equal to
![A=[AB*BC]](https://img.qammunity.org/2020/formulas/mathematics/high-school/t5mnrhaycxy2rslskxglovea6qvwth2zmo.png)
substitute
![A=[4*9]=36\ units^(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/zct71qn12le80td27njemfd5kht5syl5jd.png)
Part 8) Calculate the area of right triangle ABC
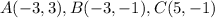
step 1
Find the distance AB
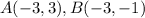
substitute in the formula
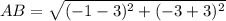
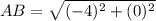
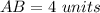
step 2
Find the distance BC
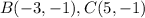
substitute in the formula
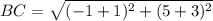
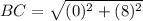
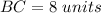
step 3
Find the distance AC
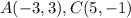
substitute in the formula
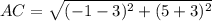
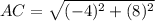
 -----> is the hypotenuse
-----> is the hypotenuse
step 4
Find the area
The area is equal to

substitute
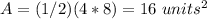
Part 10) Calculate the area of triangle ABC
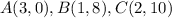
step 1
Find the distance AB
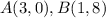
substitute in the formula
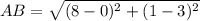
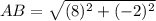
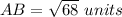
step 2
Find the distance BC
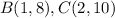
substitute in the formula


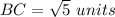
step 3
Find the distance AC
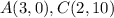
substitute in the formula
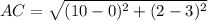
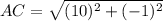
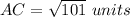
step 4
we know that
Heron's Formula is a method for calculating the area of a triangle when you know the lengths of all three sides.
Let
a,b,c be the lengths of the sides of a triangle.
The area is given by:

where
p is half the perimeter
p=
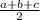
we have
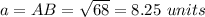
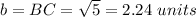
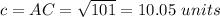
p=

Find the area