Question

What are the solutions to the system of equations? Y=x^2-7x+12 and y=-x+7

Answer 1

`\bf \begin{cases} y=x^2-7x+12\\ y=-x+7 \end{cases}\implies \stackrel{y}{x^2-7x+12}=\stackrel{y}{-x+7} \\\\\\ x^2-6x+12=7\implies x^2-6x+5=0 \\\\\\ (x-5)(x-1)=0 \implies \blacktriangleright x= \begin{cases} 5\\ 1 \end{cases} \blacktriangleleft \\\\[-0.35em] ~\dotfill`

`\bf y=-x+7\implies \stackrel{x=5}{y=-(5)+7}\implies \blacktriangleright y=2\blacktriangleleft \\\\\\ y=-x+7\implies \stackrel{x=1}{y=-(1)+7}\implies \blacktriangleright y=6 \blacktriangleleft \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ ~\hfill (5,2)\qquad (1,6)~\hfill`

Answer 2

`(5, 2)`,
`(1, 6)`

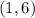
Explanation:

We have a system composed of two equations

The first is a quadratic equation and the second is a linear equation.

`y=x^2-7x+12`

`y=-x+7`

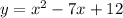
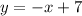
To solve the system, equate both equations and solve for x

`x^2-7x+12 = -x+7\\\\x^2 -6x +5=0`

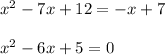
To solve the quadratic equation we must factor it.

You should look for two numbers a and c that when multiplying them obtain as result 5 and when adding both numbers obtain as result -6.

This is:

`a * c = 5\\a + c = -6`

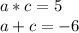
The numbers searched are -5 and -1

So

`x^2 -6x +5 = (x-5)(x-1) = 0`

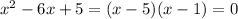
Finally the solutions to the system of equations are:

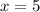`x= 5`,
`x=1`