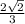Answer:
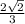
Explanation:
The sine of an angle is defined as the ratio between the opposite side and the hypotenuse of a given right-angled triangle;
sin x = ( opposite / hypotenuse)
The opposite side to the angle x is thus 1 unit while the hypotenuse is 3 units. We need to determine the adjacent side to the angle x. We use the Pythagoras theorem since we are dealing with right-angled triangle;
The adjacent side would be;
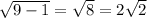
The cosine of an angle is given as;
cos x = (adjacent side / hypotenuse)
Therefore, the cos x would be;