Answer:
Sn = ∑ 4(-6)^n, from n = 0 to n = n
Explanation:
* Lets study the geometric pattern
- There is a constant ratio between each two consecutive numbers
- Ex:
# 5 , 10 , 20 , 40 , 80 , ………………………. (×2)
# 5000 , 1000 , 200 , 40 , …………………………(÷5)
- The sum of n terms is Sn =
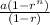 , where
, where
a is the first term , r is the common ratio between each two
consecutive terms and n is the numbers of terms
- The summation notation is ∑ a r^n, from n = 0 to n = n
* Now lets solve the problem
∵ The terms if the sequence are:
4 , -24 , 144 , -864 , ........
∵
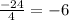
∵

∴ There is a constant ratio between each two consecutive terms
∴ The pattern is geometric
- The first term is a
∴ a = 4
- The constant ratio is r
∴ r = -6
∵ Sn =
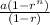
∴ Sn =
![(4(1-(-6)^(n)))/((1-(-6)))=(4(1-(-6)^(n)))/((1+6))=(4)/(7)[1-(-6)^(n)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/qsmt9tm4bgm4vv4bcvl8h11ckfpttdf7sh.png)
- By using summation notation
∵ Sn = ∑ a r^n , from n = 0 to n = n
∴ Sn = ∑ 4(-6)^n