Question

Write the sum using summation notation, assuming the suggested pattern continues. 4-24+144-864+...

Answer 1

`a_n = (4)(-6)^(n-1), n =1,2,3,4,....`

And we can verify:

`n=1 , a_1 = 4 (-6)^(1-1)= 4`

`n=2 , a_2 = 4 (-6)^(2-1)= -24`

`n=3 , a_3 = 4 (-6)^(3-1)= 144`

`n=4 , a_4 = 4 (-6)^(4-1)= -864`

And finally we can write the summation like this:

`S_n = \sum_(i=1)^n 4 (-6)^(n-1) , n =1,2,3,...`

Explanation:

For this case we have the following pattern of numbers :

4-24+144-864+...

And we want to express the sum in terms of a summation.

We can use the fact the the general term for the sum can be expressed as:

`a_n = a_1 r^(n-1)`

And for this case we can identify the value of r dividing successive terms like this:

`r = (|24|)/(|4|)= (|144|)/(|24|)=(|864|)/(|144|)= 6`

So for this case we know that the value of r =6 and the initial value 4 would represent
`a_1 = 4`

Since the sequence is alternating with + and - signs we can express the general term like this:

`a_n = (4)(-6)^(n-1), n =1,2,3,4,....`

And we can verify:

`n=1 , a_1 = 4 (-6)^(1-1)= 4`

`n=2 , a_2 = 4 (-6)^(2-1)= -24`

`n=3 , a_3 = 4 (-6)^(3-1)= 144`

`n=4 , a_4 = 4 (-6)^(4-1)= -864`

And finally we can write the summation like this:

`S_n = \sum_(i=1)^n 4 (-6)^(n-1) , n =1,2,3,...`

Answer 2

Sn = ∑ 4(-6)^n, from n = 0 to n = n

Explanation:

* Lets study the geometric pattern

- There is a constant ratio between each two consecutive numbers

- Ex:

# 5 , 10 , 20 , 40 , 80 , ………………………. (×2)

# 5000 , 1000 , 200 , 40 , …………………………(÷5)

- The sum of n terms is Sn =
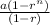`(a(1-r^(n)))/((1-r))`, where

a is the first term , r is the common ratio between each two

consecutive terms and n is the numbers of terms

- The summation notation is ∑ a r^n, from n = 0 to n = n

* Now lets solve the problem

∵ The terms if the sequence are:

4 , -24 , 144 , -864 , ........

∵
`(-24)/(4)=-6`

∵
`(144)/(-24)=-6`

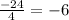
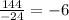
∴ There is a constant ratio between each two consecutive terms

∴ The pattern is geometric

- The first term is a

∴ a = 4

- The constant ratio is r

∴ r = -6

∵ Sn =
`(a(1-r^(n)))/((1-r))`

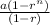
∴ Sn =
`(4(1-(-6)^(n)))/((1-(-6)))=(4(1-(-6)^(n)))/((1+6))=(4)/(7)[1-(-6)^(n)]`

- By using summation notation

∵ Sn = ∑ a r^n , from n = 0 to n = n

∴ Sn = ∑ 4(-6)^n