$3.50 and $7.25. In the movie theater the price of a drink is $3.50 and the price of a bag of pop corn is $7.25.
To solve this problem we have to use a system of equations and use a method to find the value of the unknows.
John spends a total of $61.25 on 3 drinks and 7 bags of pop corn. So, we can represent the spends as an equation of the form 3d + 7p = 61.25, where d represent drinks, p the bags of pop corn, and 61.25 the total spent.
Samuel spends a total of $107.25 on 12 drinks and 9 bags of pop corn. In the same way we can represent the spends as an equation of the form 12d + 9p = 107.25, where d represent drinks, p the bags of pop corn, and 107.25 the total spent.
Both John and Samuel spent in the same movie theater, which means both equations have a relation so we can group them into a system of equations and thus find the price of one drink and one bag of pop corn.
Writing the system of equations:
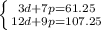
Then, we have to solve the system of equations, for this problem we going to use the substitution method which consist basically solve one of the equations for either d or p, substitute the result into the other equation, solve the new equation, and use the result to solve the other variable.
Solve the first equation for d:
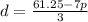
Substituting the result into the second equation:
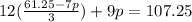
Solve the new equation for p:
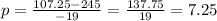
Substituting the result of the variable p in the first equation:

Solve the equation for d:
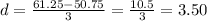
Checking the results, with d = 3.50 and p = 7.25:

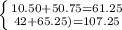
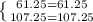 Satisfying the equals of the system of equations.
Satisfying the equals of the system of equations.