2x²+x-3. The quotient resulting of the division of the polynomial
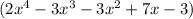 ÷
÷
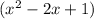 is 2x²+x-3.
is 2x²+x-3.
In order to find the quotient we have to apply the division of the polynomial
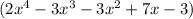 ÷
÷
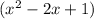 is 2x²+x-3.
is 2x²+x-3.
We divide the first monomial of the dividend
 between the first monomial of the divisor
between the first monomial of the divisor
 .
.
(2x^{4})÷
 =
=
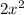
This result
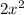 is put under the box and we multiply it by each term of the divisor polynomial and the result is subtracted in the polynomial dividend:
is put under the box and we multiply it by each term of the divisor polynomial and the result is subtracted in the polynomial dividend:
2x^4 -3x^3 -3x^2 +7x -3 ║ x^2 -2x +1
-2x^2+4x^3 -2x^2 ║ 2x^2+x-3 -----------> This is the quotient
x^3 -5x^2 +7x -3
-x^3 +2x^2 - x +0
-3x^2 +6x -3
3x^2 -6x +3
0