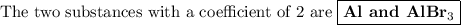Question

Consider the unbalanced chemical equation HBr + Al AlBrs + H2. When

coefficients are added to balance the equation, which two substances will
have a coefficient of 2?

Answer 1

If we balance the reaction.Then it seems like

6HBr + 2Al > 2AlBr3 +3H2

where, Al and AlBr3 has their coefficient of 2.

Answer 2

`\boxed{\text{Al and AlBr$_(3)$}}`

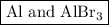
Step-by-step explanation:

Step 1. Pick the most complicated-looking formula (AlBr₃).

Put a 1 in front of it.

HBr + Al ⟶ 1AlBr₃ + H₂

Step 2: Balance Al.

We have fixed 1 Al on the right. We need 1 Al on the left.

Put a 1 in front of Al.

HBr + 1Al ⟶ 1AlBr₃ + H₂

Step 3. Balance Br.

We have fixed 3Br on the right. We need 3Br on the left.

Put a 3 in front of HBr.

3HBr + 1Al ⟶ 1AlBr₃ + H₂

Step 4. Balance H.

We have fixed 3 H on the left. We need 3 H on the right.

We need one more H (½ H₂) on the right.

3HBr + 1Al ⟶ 1AlBr₃ + ³/₂H₂

Oops. Fractional coefficients! We must multiply all coefficients by a number to give integer coefficients.

Step 5. Get rid of fractions.

Multiply all coefficients by2.

6HBr + 2Al ⟶ 2AlBr₃ + 3H₂

All species have a coefficient. The equation is now balanced.

`\text{The two substances with a coefficient of 2 are }\boxed{\textbf{Al and AlBr$_(3)$}}`