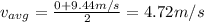Question

Modern oil tankers weigh over a half-million tons and have lengths of up to one-fourth mile. Such massive ships require a distance of 5.1 km (about 3.2 mi) and a time of 18 min to come to a stop from a top speed of 34 km/h.

(a) What is the magnitude of such a ship's average acceleration in m/s2 in coming to a stop?



(b) What is the magnitude of the ship's average velocity in m/s?

Answer 1

(a)
`-1.46\cdot 10^(-4) m/s^2`

The average acceleration of the ship is given by

`a=(v-u)/(t)`

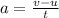
where

v is the final velocity

u is the initial velocity

t is the time elapsed

Here we have:

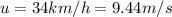`u=34 km/h =9.44 m/s` is the initial velocity

v = 0 is the final velocity

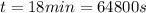`t=18 min =64800 s` is the time elapsed

Substituting, we find

`a=(0-9.44 m/s)/(64800 s)=-1.46\cdot 10^(-4) m/s^2`

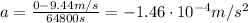
(b) 4.72 m/s

Assuming the acceleration is uniform, the average velocity of the ship is given by:

`v_(avg) = (v+u)/(2)`

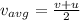
where

v is the final velocity

u is the initial velocity

Here we have:

v = 0

u = 9.44 m/s

So the average velocity of the ship is

`v_(avg) = (0+9.44 m/s)/(2)=4.72 m/s`