Answer:
The height of the prism is
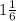 units ⇒ answer a
units ⇒ answer a
The number of blocks needed is 133 ⇒ answer c
Explanation:
* Lets explain how to solve the problem
- The volume of a rectangular prism is
→ V = Area of the base × its height
- The volume of the rectangular prism is
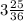 units³
units³
- The area of its base is
 units²
units²
- Substitute the values of the volume and area of the base in the rule
∴
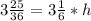
- Divide the two sides by

∴
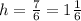 units
units
* The height of the prism is
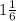 units
units
- The volume of each cubic block is
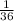 units³
units³
- The number of blocks = volume of the prism ÷ volume of the block
∵ The volume of the prism is
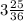 units³
units³
∵ The volume of each block is
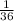 units³
units³
∴ The number of blocks =
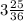 ÷
÷
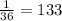
∴ The number of blocks = 133
* The number of blocks needed is 133