Question

Use the three steps to solve the problem.

The sum of 3 consecutive Integral numbers is 117. Find the numbers.
NEXT QUESTION
@
ASK FOR HELP​

Answer 1

38, 39, 40

Explanation:

Here's an interesting solution to this one. The formula to compute the nth triangular number, which is to say the sum of the first n consecutive integers, starting at 1 is

`(n(n+1))/(2)`

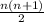
What if we wanted to start from a higher number, though? Say, 3. Well, we'd have to shift every number in the sequence up 2 (1, 2, 3 would become 3, 4, 5) so we'd be adding 2 n times. If we wanted to be more general, we could call that "shift amount" s, and our modified formula would now look like

`(n(n+1))/(2)+sn`

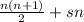
Now let's put this formula to the test. We know what our sum is here: it's 117. And we know what our n is too; we're finding 3 integers, so n = 3. This gives us the equation

`(3(3+1))/(2) +3s=117`

Solving this equation for s:

`(3(4))/(2) +3s=117\\\\(12)/(2)+3s=117\\ 6+3s=117\\3s=111\\s=37`

so our "shift amount" is 37, and our sequence gets shifted from 1, 2, 3 to 38, 39, 40.

But why?

This was a lot of setup for what seems like a disappointing payoff, but the real power with this approach is that we've actually just solved every problem of this type. Let's say you had to find the sum of 5 consecutive integers, and their sum was 70. Not a problem. Just set our n = 5 and solve:

`(5(6))/(2) +5s=70\\\\(30)/(2) +5s = 70\\15+5s=70\\5s=55\\s=11`

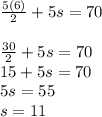
Which gives us a "shift" of 11 and the sequence 12, 13, 14, 15, 16 (which is exactly the sequence I came up with for this problem!)

Answer 2

The numbers are 38, 39, and 40

Explanation:

Let the 3 consecutive Integral numbers be;

x, x+1, x+2

We are informed that the sum of the 3 consecutive Integral numbers is 117. Therefore;

x + x+1 + x + 2 = 117

3x + 3 = 117

3x = 114

x = 38

x+1 = 39

x+2 = 40