Answer:
38, 39, 40
Explanation:
Here's an interesting solution to this one. The formula to compute the nth triangular number, which is to say the sum of the first n consecutive integers, starting at 1 is
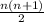
What if we wanted to start from a higher number, though? Say, 3. Well, we'd have to shift every number in the sequence up 2 (1, 2, 3 would become 3, 4, 5) so we'd be adding 2 n times. If we wanted to be more general, we could call that "shift amount" s, and our modified formula would now look like
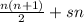
Now let's put this formula to the test. We know what our sum is here: it's 117. And we know what our n is too; we're finding 3 integers, so n = 3. This gives us the equation
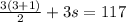
Solving this equation for s:
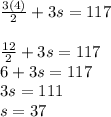
so our "shift amount" is 37, and our sequence gets shifted from 1, 2, 3 to 38, 39, 40.
But why?
This was a lot of setup for what seems like a disappointing payoff, but the real power with this approach is that we've actually just solved every problem of this type. Let's say you had to find the sum of 5 consecutive integers, and their sum was 70. Not a problem. Just set our n = 5 and solve:
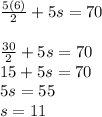
Which gives us a "shift" of 11 and the sequence 12, 13, 14, 15, 16 (which is exactly the sequence I came up with for this problem!)