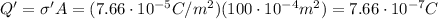Question

wo parallel plates of area 100cm2are given charges of equal magnitudes 8.9 ×10−7C but opposite signs. The electric field within the dielectric material filling the space between the plates is 1.4 ×106V/m. (a) Calculate the dielectric constant of the material. (b) Determine the magnitude of the charge induced on each dielectric surface.

Answer 1

(a) 7.18

The electric field within a parallel plate capacitor with dielectric is given by:

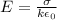`E=(\sigma)/(k \epsilon_0)` (1)

where

`\sigma` is the surface charge density

k is the dielectric constant

`\epsilon_0` is the vacuum permittivity

The area of the plates in this capacitor is

`A=100 cm^2 = 100\cdot 10^(-4) m^2`

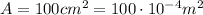
while the charge is

`Q=8.9\cdot 10^(-7)C`

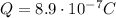
So the surface charge density is

`\sigma = (Q)/(A)=(8.9\cdot 10^(-7) C)/(100\cdot 10^(-4) m^2)=8.9\cdot 10^(-5) C/m^2`

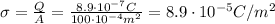
The electric field is

`E=1.4\cdot 10^6 V/m`

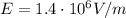
So we can re-arrange eq.(1) to find k:

`k=(\sigma)/(E \epsilon_0)=(8.9\cdot 10^(-5) C/m^2)/((1.4\cdot 10^6 V/m)(8.85\cdot 10^(-12) F/m))=7.18`

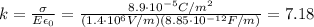
(b)
`7.66\cdot 10^(-7)C`

The surface charge density induced on each dielectric surface is given by

`\sigma' = \sigma (1-(1)/(k))`

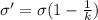
where

`\sigma=8.9\cdot 10^(-5) C/m^2` is the initial charge density

k = 7.18 is the dielectric constant

Substituting,

`\sigma' = (8.9\cdot 10^(-5) C/m^2) (1-(1)/(7.18))=7.66\cdot 10^(5) C/m^2`

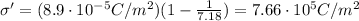
And by multiplying by the area, we find the charge induced on each surface:

`Q' = \sigma' A = (7.66\cdot 10^(-5) C/m^2)(100 \cdot 10^(-4)m^2)=7.66\cdot 10^(-7)C`