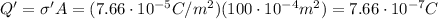(a) 7.18
The electric field within a parallel plate capacitor with dielectric is given by:
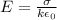 (1)
(1)
where
 is the surface charge density
is the surface charge density
k is the dielectric constant
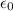 is the vacuum permittivity
is the vacuum permittivity
The area of the plates in this capacitor is
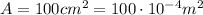
while the charge is
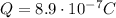
So the surface charge density is
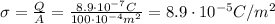
The electric field is
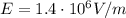
So we can re-arrange eq.(1) to find k:
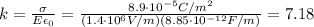
(b)
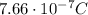
The surface charge density induced on each dielectric surface is given by
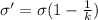
where
 is the initial charge density
is the initial charge density
k = 7.18 is the dielectric constant
Substituting,
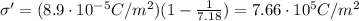
And by multiplying by the area, we find the charge induced on each surface: