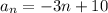Answer:
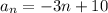
Explanation:
The arithmentic function formula is:
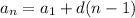
Let's plug in what we know.
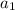 (the first term in our sequence) is 7. d (the common difference) is -3. This means we are subtracting 3 every time.
(the first term in our sequence) is 7. d (the common difference) is -3. This means we are subtracting 3 every time.
Plugging that in to the formula, we get

Now we distribute and combine like terms.
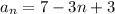

Change the order to fit the format and you get