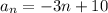Question

Find a formula for the nth term in this

arithmetic sequence:
a₁ = 7, a2 = 4, a3 = 1, a4 = -2, ...
an
=
[?]n +

Answer 1

The formula for the nth term in this arithmetic sequence is:

-3n + 10

Answer 2

`a_(n) = -3n + 10`

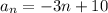
Explanation:

The arithmentic function formula is:

`a_(n) = a_(1) + d(n-1)`

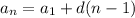
Let's plug in what we know.
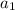`a_(1)` (the first term in our sequence) is 7. d (the common difference) is -3. This means we are subtracting 3 every time.

Plugging that in to the formula, we get

`a_(n) = 7 -3(n-1)`

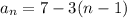
Now we distribute and combine like terms.

`a_(n) = 7 - 3n +3`

`a_(n) = 10 - 3n`

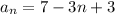
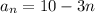
Change the order to fit the format and you get

`a_(n) = -3n + 10`