Question

Which of the following describes the roots of the polynomial function K x) - (x+ 2)(x-4)(x+1)3?

Answer 1

It's the first option.

Explanation:

(x + 2)^2 gives a duplicate (multiplicity 2) root. (because (x + 2)^2 = 0 so x = -2 multplicity 2)

(x - 4) gives one root of 4.

(x + 1)^3 gives x = -1 with multiplicity 3.

Answer 2

-2 with multiplicity 2, 4 with multiplicity 1, and -1 with multiplicity 3.

Explanation:

The given polynomial function is:
`f(x)=(x+2)^2(x-4)(x+1)^3`.

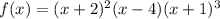To find the roots of this polynomial, we equate each factor to zero.

This implies that;

i.
`(x+2)^2=0`,
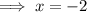`\implies x=-2`, the multiplicity of this root is 2, because the factor repeats twice

ii.
`x-4=0`,
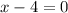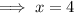`\implies x=4`, the multiplicity of this root is 1, because the factor repeats once.

ii.
`(x+1)^3=0`,
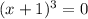`\implies x=-1`, the multiplicity of this root is 3, because the factor repeats three times.