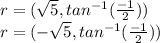Answer:
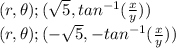
Explanation:
Here we are given our rectangular coordinates as (2,-1) . We have to convert this into polar coordinates. The formula for conversion into polar form is
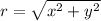
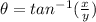
Substituting the values of x and y in the above formulas we get
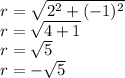
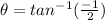
Hence our polar coordinates are