Question

Which trigonometric function requires a domain restriction of [-pi/2, pi/2] to make it invertable?

Answer 1

A)
`f(x)=sin x`

Explanation:

I just did the test and this was the correct answer.

Answer 2

`y=\tan x`

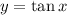
Explanation:

The trigonometric function that needs a domain restriction of
`[-(\pi)/(2),(\pi)/(2) ]` to make it invertible is
`y=\tan x`.

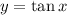The function
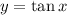`y=\tan x` will pass the horizontal line test on this interval therefore making it an invertible function on this interval.

This explains why the inverse tangent function,
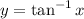`y=\tan^(-1) x` has range
`[-(\pi)/(2),(\pi)/(2) ]`.