Question

Polygon YYY is a scaled copy of Polygon XXX using a scale factor of \dfrac13 3 1 ? start fraction, 1, divided by, 3, end fraction. Polygon YYY's area is what fraction of Polygon XXX's area?

Answer 1

1/9

Explanation:

(1/3)^2 = 1/3 x 1/3 =1/9

plus I checked the answer after I got it wrong so...

Answer 2

`(1)/(9)`

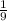
Explanation:

This is a case of enlargement of a figure of scale factor
`(1)/(3)`.

In any enlargement,
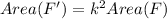`Area(F')=k^2 Area(F)`, where the transformation maps F onto F'.

In this case, let F be polygon XXX and let F' be polygon YYY. Hence,

`Area(YYY) = k^2 Area (XXX)`

`Area(YYY) = ((1)/(3))^2 Area(XXX)`

`Area(YYY) = (1)/(9) Area(XXX)`

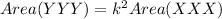
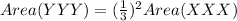
Therefore, the area of polygon YYY is
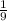`(1)/(9)` of the area of polygon XXX.