Answer:
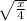 and
and
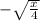
Explanation:
The function is given as
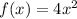
to find inverse, we follow the steps shown below:
1. write "y" in place of "f(x)"
2. interchange "x" and "y"
3. solve for the new "y"
4. replace y with f^-1(x)
Let's do this:

These 2 are the inverse functions.