Question

What is the length of the shortest side of a triangle that has vertices at (-6, -5), (-5, 6), and (-2, 2)? A. B. C. D.

Answer 1

5 units

Explanation:

Draw the triangle with the vertices given. Identify the smallest side and draw in a right triangle using the smallest side of the original triangle as the hypotenuse of the right triangle, as shown on the grids below.

The horizontal side of the small right triangle measures 3 units and the vertical side of the small right triangle measures 4 units.

Use the Pythagorean theorem to find the length of the hypotenuse.

Therefore, the length of the shortest side of the triangle measures 5 units.

3^2 + 4^2 = c^2

9 + 16 = c^2

25 = c^2

5 = c

Answer 2

5

Explanation:

We can use the distance formula with 3 different vertices to figure out the shortest of the three sides.

The distance formula is
`√((y_2-y_1)^2+(x_2-x_1)^2)`

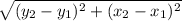
Where (x_1,y_1) is the first points and (x_2,y_2) is the second set of points, respectively.

Now let's figure out the length of 3 sides.

1. The length between (-6,-5) & (-5,6):

`√((y_2-y_1)^2+(x_2-x_1)^2) \\=√((6--5)^2+(-5--6)^2)\\ =√((6+5)^2+(-5+6)^2) \\=√(11^2+1^2) \\=√(122)`

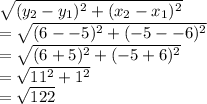
2. The length between (-6,-5) & (-2,2):

`√((y_2-y_1)^2+(x_2-x_1)^2) \\=√((2--5)^2+(-2--6)^2) \\=√((2+5)^2+(-2+6)^2)\\ =√(7^2+4^2)\\ =√(65)`

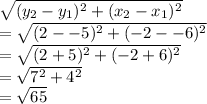
3. The length between (-5,6) & (-2,2):

`√((y_2-y_1)^2+(x_2-x_1)^2) \\=√((2-6)^2+(-2--5))^2}\\ =√((-4)^2+(3)^2) \\=√(25) \\=5`

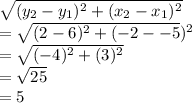
Thus, length of the shortest side is 5.