Answer:
5
Explanation:
We can use the distance formula with 3 different vertices to figure out the shortest of the three sides.
The distance formula is
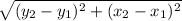
Where (x_1,y_1) is the first points and (x_2,y_2) is the second set of points, respectively.
Now let's figure out the length of 3 sides.
1. The length between (-6,-5) & (-5,6):
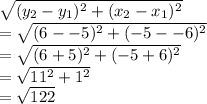
2. The length between (-6,-5) & (-2,2):
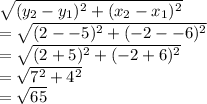
3. The length between (-5,6) & (-2,2):
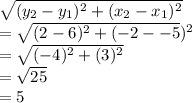
Thus, length of the shortest side is 5.