Answer:
The sequence is not a geometric sequence
Explanation:
In a geometric sequence you find the following term multiplying the current by a fixed quantity called the common ratio.
To prove if a sequence is geometric we need to check if the ratio is consistent across the sequence. To check for the ratio we use the formula:
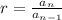
were
 is the ratio
is the ratio
 is the current term
is the current term
 is the previous term
is the previous term
Let's star with 1, so
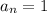 and
and
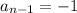
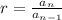
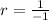
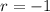 .
.
Now let's check 4 and 1, so
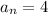 and
and

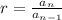

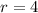
Since the ratios between two pair of numbers are different, we can conclude that the sequence is not geometric.